[5]

Finally, turtle graphics

In part 4 we were doing some refactoring just to keep the house in order before we move to greater things. We’ve managed to do a repeat loop in the parser and we introduced for the first time the interpreter which will tie up together everything else.

There are still many things to do, possibly the most pressing having a proper tokenizer, but as a developer we want to do what we want to do and that’s to have a turtle responding to our commands, in this case to draw a square to start with!

For the turtle we need to add a canvas to the html. To make it all more LOGO related I will call the canvas logo-graphics. This is also a good time to rename the editor from myTextarea to logo-editor.

<textarea id="logo-editor">repeat 4 [ fd 60 rt 90 ]</textarea>
<canvas id="logo-graphics" width="400" height="400"></canvas>

We make the canvas 400 x 400, mostly because it is small and 400 is easy divisible to 200, 100, 50, 25, all integers.

If we run it, we won’t see the canvas! we will try to add a border in the css file just to know where it is. The only concession I do is to put some background colour to it. At this point we don’t need to do any “beautification” to the html (no premature optimization, even how tempting it is), so we will focus in the turtle.

#logo-graphics {
  border: 2px solid black;
  background-color: #E8E8E8;
}

We add the canvas to the interpreter as well:

constructor(editorId, canvasId, aliases) {
  this.editor = document.getElementById(editorId);
  this.canvas = document.getElementById(canvasId);
  this.tokenizer = new Tokenizer(aliases);
  this.parser = new Parser();
}

and

const interpreter = new Interpreter('logo-editor', 'logo-graphics', primitiveAliases);
interpreter.run();

The final result is

The turtle 🐢

For the turtle, the easiest way is to draw everything in the parser when we execute the primitives fd and rt. For me this will pollute the parser with information about the canvas that it doesn’t need to know, it is much better to create a function (or a class) Turtle and instantiate this in the parser instead:

So here it is our class:

class Turtle {
  constructor(canvasObject) {
    console.log("🐢");
  }
}

And the interpreter:

this.parser = new Parser(this.canvas);

and we finally create a constructor in the parser:

constructor(canvasObject) {
  this.turtle = new Turtle(canvasObject);
}

Drawing the graphics

We will start with one canvas where we will draw the turtle and the graphics. Later on we will find out the best way to keep the graphics under the turtle while we move the turtle like a sprite around without interfering with the background.

For now in the turtle:

class Turtle {
  constructor(canvasObject) {
    console.log("🐢");
    this.ctx = canvasObject.getContext('2d');
    this.width = canvasObject.width;
    this.height = canvasObject.height;
  }
}

And we will mimic the two methods we have in Parser for the two primitives that draw something, execute_forward() and execute_right() and we will call them from the parser. For now they are empty, so we see if they do anything.

 execute_forward(n = 0) {
  console.log(`[Turtle] - execute_forward(${n})`);
}
execute_right(deg = 0) {
  console.log(`[Turtle] - execute_right(${deg})`);
}

And in the parser:

execute_forward(n = 0) {
  console.log(`Starting: execute_forward ${n}`);
  this.turtle.execute_forward(n);
}
execute_right(n = 0) {
  console.log(`Starting: execute_right ${n}`);
  this.turtle.execute_right(n);
}

And we will see in the logs that they are effectively being called. This is really exciting (at least for me) because we are about to be able to draw a loop from our own programming language!!

Let’s start with the easy part. We need to position the turtle in the middle. For that we need to know the center (X) and center (Y) of the canvas. Since we are going to update the position of the turtle more than once we may as well create a method for that, followed by defining the center position in the constructor so we can reuse it.

Remember that the object is Turtle and as such the properties x and y define the position for the turtle itself. To center it, we create a new method and call it from the constructor so it will be the starting position.

this.centerX = parseInt(this.width / 2);
this.centerY = parseInt(this.height / 2);

updateTurtlePosition(x = 0, y = 0) {
  this.x = x;
  this.y = y;
}
centerTurtle() {
  this.updateTurtlePosition(this.centerX, this.centerY);
}

execute_forward(n = 0) {
  console.log(`[Turtle] - execute_forward(${n})`);
  let x1 = this.x;
  let y1 = this.y + n;

  this.ctx.lineWidth = 1;
  this.ctx.beginPath();
  this.ctx.moveTo(this.x, this.y);
  this.ctx.lineTo(x1, y1);
  this.ctx.stroke();
  
  this.updateTurtlePosition(x1, y1);
}

and to see the turtle moving forward (we don’t care right now about angles, I just want to see if it works), we can do in execute_forward():

and this is the most beautiful sight ever, 4 lines put one after another and getting out of the canvas because from the center to the top is 400/2 = 200 pixels and if each step is 60 pixels in the fd 60 we are out of the canvas (60 x 4 = 240). I am surprised that it goes down, I was expecting the line to go up instead.

But before that I’ve just realized that instead of a 🐢 in the console I get 🐢. The reason is simple, in the html we didn’t define the we are working with UTF8, so if we add in the head element:

<meta charset="UTF-8">

Not only we could see in the future emojis in the screen but this also fixes the emojis in the console (weird!).

Moving the turtle. Understanding coordinates in canvas

Before that, let’s set the value of the angle in execute_right(). The turtle has properties x and y for coordinates and the turtle is facing whatever angle we move it, so we can have that angle property. Angle doesn’t mean much for a turtle, so we will call it orientation and it will be in degrees (more on that later).

For orientation, 0 degrees will mean facing up (what in normal coordinates is 90°) and since we are dealing with the right primitive, any movements to the right from there is a positive angle.

Since we have the method updateTurtlePosition() we can name the next one updateTurtleOrientation(). But wait a second, careful with the names. Updating would mean for a normal person that we are replacing the current value with a new value, however what we do is we increase (or decrease) the current orientation, so if before we were facing rt 30 and later we have rt 20 the total angle that the turtle has rotated is 30 + 20 = 50, so the orientation is 50. If we say updateTurtleOrientation() we may think that we replace the value 30 with 20. Something like incrementTurtleOrientation() or rotateTurtleBy(). I want to be as explicit as possible so incrementTurtleOrientation() seems the correct one to me

incrementTurtleOrientation(deg = 0) {
  this.orientation += deg;
}

To make completely sure that we know that the orientation is in degrees and not radians I called the argument deg instead of the usual angle, and we add it to the constructor:

this.orientation = 0;

And now about the coordinates:

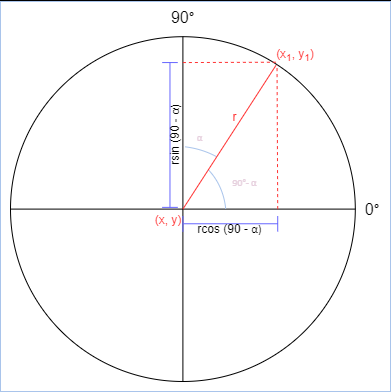
When we are facing up, the angle in normal coordinates is 90°. If we move 30° to the right with rt 30 the angle in normal coordinates is really 90° - 30° = 60°. So the angle (we will call it α) we deal in our trigonometry is really 90 - α. If the value we move in fd primitive is called r (because it is the radius of a circle as in the picture), when starting in a point (x, y) the new coordinates are:

x1 = x + r·cos(90-α)
y1 = y + r·sin(90-α)

This can be simplified even more because cos(90-α) = sin(α) and sin(90-α) = cos(α), so we will have:

x1 = x + r·sin(α)
y1 = y + r·cos(α)

Let’s do that in the code:

execute_forward(n = 0) {
  console.log(`[Turtle] - execute_forward(${n})`);
  let x1 = this.x + n * Math.sin(this.orientation);
  let y1 = this.y + n * Math.cos(this.orientation);

  this.ctx.lineWidth = 1;
  this.ctx.beginPath();
  this.ctx.moveTo(this.x, this.y);
  this.ctx.lineTo(x1, y1);
  this.ctx.stroke();
  
  this.updateTurtlePosition(x1, y1);
}

Note that we don’t update or increase the orientation; moving forward just moves forward at whatever angle we are facing. If we run it (we can’t wait, can we?) we still get the same line facing down! The reason is that we forgot to put some code in execute_right:

execute_right(deg = 0) {
  console.log(`[Turtle] - execute_right(${deg})`);
  this.incrementTurtleOrientation(deg);
}

And now when we run it we get… a rubbish triangle!

What happened? if we put a log in incrementTurtleOrientation() we see that the values are correct: 90, 180, 270, 360.

To avoid losing you for a couple of hours debugging, the issue is that all the trigonometric functions use radians instead of degrees and we passed the values in degrees. We add this inside Turtle, which will help with any conversion in the future.

DEGREE_TO_RADIAN = Math.PI / 180;
toRadians = (deg = 0) => Number(deg * this.DEGREE_TO_RADIAN);

And in execute_forward():

let alpha = this.toRadians(this.orientation);
let x1 = this.x + n * Math.sin(alpha);
let y1 = this.y + n * Math.cos(alpha);

And we got our square!!! this is the time that we want to start playing instead of just having a square on the screen. Since we have an editor (just a textarea element), we can add a run button that will execute anything we put in the editor textarea.

In the html, we add the button:

<button onclick="interpreter.run()">run</button>

This is the time we are happy that we had a method in the interpreter to run the script in the textarea, which makes everything very tidy. So we play around with fd 100 and we see that it goes down instead of up again!

The problem is that since our origin of coordinates is top-left corner in canvas, y grows down instead of growing up. So instead of

let y1 = this.y + n * Math.cos(alpha);

we need to change the sign of the “increment”

let y1 = this.y - n * Math.cos(alpha);

And finally (just finally) we can rest since our square is drawn in the correct coordinates using a repeat primitive.

In the next part we will finally see the turtle (well, just a circle or triangle instead of a turtle) and we will work on not messing the drawings with extra turtles everywhere!